3.1 DEFINITION DU FILTRE PASSE-BANDE NORMALISE

A partir du cahier des charges on commence par déterminer le type et l’ordre du filtre prototype passe-bas le mieux adapté à nos
contraintes.

Selon la théorie générale des filtres décrite dans l’ouvrage « Reference Data for Engineers », on procède en définissant d’abord les
fréquences suivantes :

Pour appliquer la transformation du prototype passe-bas vers le prototype passe-bande, on doit avoir un gabarit de filtrage
symétrique, c’est-à-dire que la relation suivante doit être respecter :

Avec les valeurs initiales cette relation n’est pas vérifiée. Il faut donc symétriser le gabarit de filtrage en définissant par exemple
une nouvelle fréquence fs- tel que :

on obtient f-s = 4,95 GHz et fref = 6,197 GHz.

On peut maintenant calculer la fréquence normalisé d’atténuation du filtre prototype passe-bas correspondant à notre gabarit à
l’aide de la relation suivante :

soit .

Le type de filtre le mieux adapté à notre situation est le prototype de Tchebycheff car sa pente d’atténuation hors bande est plus
importante que celle du prototype de Butterworth.
Le prototype de Butterworth présente des variations de temps de propagation de groupe meilleures, mais cet aspect n’est pas
déterminant dans notre cas puisque l’on transmet une porteuse pure.

On extrait du cours sur les filtres micro-ondes les relations exposées dans la suite de l’analyse théorique.
Pour calculer l’ordre minimum du filtre à réaliser on doit fixer le niveau des pertes d’insertion (dans la bande passante). Pour déterminer
celles-ci on considère que le filtre est sans pertes afin d’utiliser la relation |S11|²+ |S21|² = 1.

On s’aperçoit que le paramètre |S11|dB < -18dB (coefficient de réflexion) est plus contraignant que les pertes d’insertion
(|S21|dB < -1dB).
On fixe pour |S11|dB une valeur meilleure que celle du cahier des charges pour avoir une marge pour compenser les tolérances de
réalisation du filtre.
On choisit |S11|dB= -26dB, d’où on en déduit Am= |S21|dB = -0,01dB.

De la même manière on fixe pour la réjection une marge de 5dB, soit As= 25dB.
Connaissant , As et Am, on peut en déduire l’ordre n minimum d’un filtre de type Tchebycheff avec la relation :

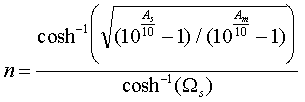On obtient n = 2,51. On choisit donc un filtre d’ordre 3.

Avec un filtre d’ordre 3 et Am = 0,01dB, on peut calculer la nouvelle valeur de As avec la relation suivante :

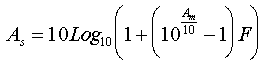	page 4
SOMMAIRE